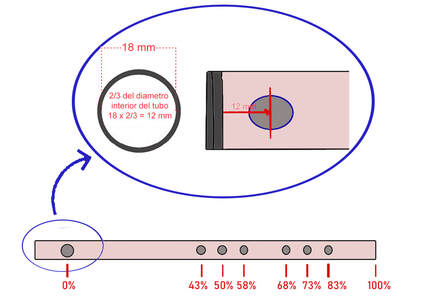
La aritmética de las escalas
Cuando fabricas un instrumento de cuerda, como un ukelele o una guitarra, la parte más difícil es saber dónde colocar los trastes para poder tocar con afinación. Tradicionalmente, para calcular la colocación de los trastes en el mástil, los luthieres utilizaban la regla del 18.
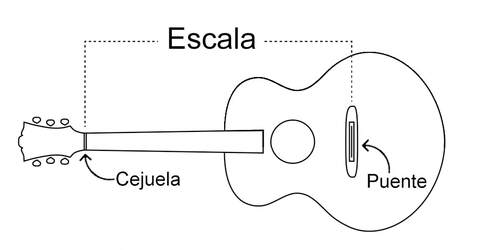
Para empezar, hay que medir en milímetros la escala (L), que es la distancia entre la cejuela y el puente.
Para calcular la distancia entre la cejuela y el primer traste, hay que dividir la longitud de escala por 18. El número 18 se conoce por "la constante de temperamento”. Para calcular la posición de los siguientes trastes, se hace lo mismo pero tomando en cuenta la distancia hasta el traste anterior.
Si la escala (L) es 300 mm, entonces:
L = 300 mm
L1 (1º traste) = L/18 = 300 / 18 = 16,7 mm (1,7 cm)
L2 (2º traste) = L1 + ((L- L1) / 18) = 16,7 + ((300 - 16,7) / 18) = 32,4 mm (3,2 cm)
L3 (3º traste) = L2 + ((L- L2) / 18) = 32,4 + ((300 – 32,4) / 18) = 47,3 mm (4,7 cm)
L4 (4º traste) = L3 + ((L- L3) / 18) = 47,3 + ((300 – 47,3) / 18) = 61,3 mm (6,1 cm)
Etc.
Siempre se miden las distancias desde la cejuela.
Por si quieres fabricar un instrumento profesional, la regla del 18 no es muy precisa y, como se ve en el ejemplo de arriba, he redondeado las cifras. Para lograr una mejor precisión, en lugar de 18 hay que usar la constante: 17.817.
Si no tienes calculadora y quieres comprobar las respuestas, se puede utilizar la calculadora automática:
https://aprendizdeluthier.com/como-calcular-la-posicion-de-los-trastes-en-el-diapason/
Si tienes una guitarra o ukelele, se puede comprobar con una regla si está bien hecho.
Para empezar, hay que medir en milímetros la escala (L), que es la distancia entre la cejuela y el puente.
Para calcular la distancia entre la cejuela y el primer traste, hay que dividir la longitud de escala por 18. El número 18 se conoce por "la constante de temperamento”. Para calcular la posición de los siguientes trastes, se hace lo mismo pero tomando en cuenta la distancia hasta el traste anterior.
Si la escala (L) es 300 mm, entonces:
L = 300 mm
L1 (1º traste) = L/18 = 300 / 18 = 16,7 mm (1,7 cm)
L2 (2º traste) = L1 + ((L- L1) / 18) = 16,7 + ((300 - 16,7) / 18) = 32,4 mm (3,2 cm)
L3 (3º traste) = L2 + ((L- L2) / 18) = 32,4 + ((300 – 32,4) / 18) = 47,3 mm (4,7 cm)
L4 (4º traste) = L3 + ((L- L3) / 18) = 47,3 + ((300 – 47,3) / 18) = 61,3 mm (6,1 cm)
Etc.
Siempre se miden las distancias desde la cejuela.
Por si quieres fabricar un instrumento profesional, la regla del 18 no es muy precisa y, como se ve en el ejemplo de arriba, he redondeado las cifras. Para lograr una mejor precisión, en lugar de 18 hay que usar la constante: 17.817.
Si no tienes calculadora y quieres comprobar las respuestas, se puede utilizar la calculadora automática:
https://aprendizdeluthier.com/como-calcular-la-posicion-de-los-trastes-en-el-diapason/
Si tienes una guitarra o ukelele, se puede comprobar con una regla si está bien hecho.
Agujeros y porcentajes:
Una flauta travesera simple de PVC, bambú o incluso cartón es relativamente fácil de fabricar pero puede ser complicada de tocar.
Siempre se empieza la fabricación con la boquilla, el centro de la cual debería medir 2/3 del diámetro interior del tubo desde el extremo taponado (como se muestra en el dibujo). Una vez hecha la boquilla, hay que soplar para ver en que tono suena la flauta: se puede subir el tono hasta encontrar la nota que quieras, acortando el tubo. Se recomienda cortar muy poco a poco para no pasarse: es fácil subir el tono pero es difícil bajarlo. Cuando esté afinada, hay que medir la longitud de la escala (L) que es la distancia entre la mitad del agujero de la boquilla y la base de la flauta. Calcular los agujeros con precisión es muy complicado porque hay que tomar en cuenta muchos factores, pero se puede calcular la posición de forma aproximada utilizando porcentajes. El medio de la boquilla es 0% y el extremo es 100%. Los agujeros, entonces se encuentra en las siguientes posiciones: A1 = 43% A2 = 50% A3 = 58% A4 = 68% A5 = 73% A6 = 83% Conviene hacer los agujeros pequeños y luego agrandarlos para obtener el tono deseado. Recomiendo empezar con el cuarto agujero porque, si no da el tono deseado, es relativamente fácil adaptarlo. Si lo abres hacia arriba subirá el tono de la nota. En el caso de tener que bajar el tono, se puede cubrir la parte superior del agujero con un trozo de cinta adhesiva. Este método de calcular la posición de los agujeros no es el más preciso pero puede valer para una actividad en el aula. Si los porcentajes no parecen funcionar, entonces ¡hay que experimentar! |
Los compases y las fracciones:
Los compases son una manera maravillosa de introducir las divisiones y las multiplicaciones a una clase. Al final se enseñan las mates de siempre pero, al estar disfrazado como música (que pueden tocar con las palmas), puede motivar a algunos estudiantes: es un ejemplo de enseñanza multisensorial y transversal.
Para facilitar los cálculos, se aconseja utilizar como base un compás de 4/4, que consiste en una redonda. Entonces hay que explicar que:
1 redonda = 2 blancas = 4 negras = 8 corcheas = 16 x semicorcheas = 32 fusas
Si lo traducimos a fracciones, entonces una redonda = 1, una blanca = 1/2, una negra = 1/4, una corchea = 1/8, una semicorchea = 1/16 y una fusa = 1/32
Juego 1: Palmas
Muestra una partitura a los estudiantes y, con ellos, calcula como se divide cada compás. Entonces, con las palmas, marca el ritmo. Con este juego se puede introducir diferentes compases (3/4 o 6/8) e incluso hacer patrones de canciones para ver si los estudiantes adivinan de que canción se trata.
Juego 2: Sumar y restar fracciones
Pon unos compases de 4/4 (1 redonda) en los que falten notas y los estudiantes tienen que calcular cuales faltan (ej. un compás que contiene 1 negra, 3 corcheas y 5 semicorcheas (1/4 + 1/8 + 6/16) falta 1 negra (1/4) para completarse. Este juego puede ser más divertida con fragmentos de canciones conocidas.
Para facilitar los cálculos, se aconseja utilizar como base un compás de 4/4, que consiste en una redonda. Entonces hay que explicar que:
1 redonda = 2 blancas = 4 negras = 8 corcheas = 16 x semicorcheas = 32 fusas
Si lo traducimos a fracciones, entonces una redonda = 1, una blanca = 1/2, una negra = 1/4, una corchea = 1/8, una semicorchea = 1/16 y una fusa = 1/32
Juego 1: Palmas
Muestra una partitura a los estudiantes y, con ellos, calcula como se divide cada compás. Entonces, con las palmas, marca el ritmo. Con este juego se puede introducir diferentes compases (3/4 o 6/8) e incluso hacer patrones de canciones para ver si los estudiantes adivinan de que canción se trata.
Juego 2: Sumar y restar fracciones
Pon unos compases de 4/4 (1 redonda) en los que falten notas y los estudiantes tienen que calcular cuales faltan (ej. un compás que contiene 1 negra, 3 corcheas y 5 semicorcheas (1/4 + 1/8 + 6/16) falta 1 negra (1/4) para completarse. Este juego puede ser más divertida con fragmentos de canciones conocidas.
